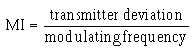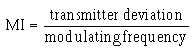2-24
AMOUNT OF PHASE SHIFT IS PROPORTIONAL TO THE AMPLITUDE OF THE
MODULATING SIGNAL.
(If a 10-volt signal causes a phase shift of 20 degrees, then a 20-volt signal causes a phase shift of 40
degrees.)
RATE OF PHASE SHIFT IS PROPORTIONAL TO THE FREQUENCY OF THE
MODULATING SIGNAL.
(If the carrier were modulated with a 1-kilohertz tone, the carrier would advance and retard in phase
1,000 times each second.)
Phase modulation is also similar to frequency modulation in the number of sidebands that exist
within the modulated wave and the spacing between sidebands. Phase modulation will also produce an
infinite number of sideband frequencies. The spacing between these sidebands will be equal to the
frequency of the modulating signal. However, one factor is very different in phase modulation; that is, the
distribution of power in pm sidebands is not similar to that in fm sidebands, as will be explained in the
next section.
Modulation Index
Recall from frequency modulation that modulation index is used to calculate the number of
significant sidebands existing in the waveform. The higher the modulation index, the greater the number
of sideband pairs. The modulation index is the ratio between the amount of oscillator deviation and the
frequency of the modulating signal:
In frequency modulation, we saw that as the frequency of the modulating signal increased (assuming
the deviation remained constant) the number of significant sideband pairs decreased. This is shown in
views (A) and (B) of figure 2-21. Notice that although the total number of significant sidebands decreases
with a higher frequency-modulating signal, the sidebands spread out relative to each other; the total
bandwidth increases.