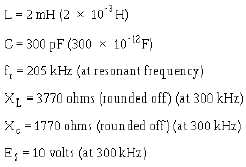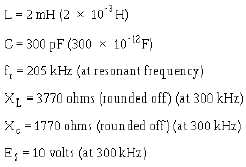1-13
In summary, in a series-LC circuit with a source voltage that is below the resonant frequency (100
kHz in the example), the resultant reactance (X), and therefore impedance, is higher than at resonance. In
addition current is lower, and the voltage drops across the reactances are lower. All of the above follow in
sequence due to the fact that XC is greater than XL at any frequency lower than the resonant frequency.
How the Ideal Series-LC Circuit Responds to a Frequency Above Resonance (300 kHz)
Given:
Again, XL and XC are not equal. This time, XL is larger than XC. (If you don't know why, apply the
formulas and review the past several pages.) The resultant reactance is 2000 ohms (XL
-
X
C
= 3770
-
1770 = 2000 ohms.) Therefore, the resultant reactance (X), or the impedance of our perfect circuit at 300
kHz, is 2000 ohms.
By applying Ohm's law as before:
In summary, in a series-LC circuit with a source voltage that is above the resonant frequency (300
kHz in this example), impedance is higher than at resonance, current is lower, and the voltage drops
across the reactances are lower. All of the above follow in sequence from the fact that X
L
is greater than
XC at any frequency higher than the resonant frequency.
Summary of the Response of the Ideal Series-LC Circuit to Frequencies Above, Below, and at
Resonance
The ideal series-resonant circuit has zero impedance. The impedance increases for frequencies higher
and lower than the resonant frequency. The impedance characteristic of the ideal series-resonant circuit
results because resultant reactance is zero ohms at resonance and ONLY at resonance. All other
frequencies provide a resultant reactance greater than zero.
Zero impedance at resonance allows maximum current. All other frequencies have a reduced current
because of the increased impedance. The voltage across the reactance is greatest at resonance because
voltage drop is directly proportional to current. All discrimination between frequencies results from the
fact that XL and XC completely counteract ONLY at the resonant frequency.