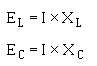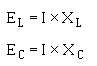1-11
Now, apply Ohm's law for a.c. circuits:
Don't be confused by this high value of current. Our perfect, but impossible, circuit has no
opposition to current. Therefore, current flow will be extremely high. The important points here are that
AT RESONANCE, impedance is VERY LOW, and the resulting current will be comparatively HIGH.
If we apply Ohm's law to the individual reactances, we can figure relative values of voltage across
each reactance.
These are reactive voltages that you have studied previously. The voltage across each reactance will
be comparatively high. A comparatively high current times 2580 ohms yields a high voltage. At any given
instant, this voltage will be of opposite polarity because the reactances are opposite in effect. EL + EC =
zero volts
WARNING
THE INDIVIDUAL VOLTAGES MAY REACH QUITE HIGH VALUES.
ALTHOUGH LITTLE POWER IS PRESENT, THE VOLTAGE IS REAL AND
CARE SHOULD BE TAKEN IN WORKING WITH IT.
Let's summarize our findings so far. In a series-LC circuit with a resonant-frequency voltage applied,
the following conditions exist:
XL and XC are equal and subtract to zero.
Resultant reactance is zero ohms.
Impedance (Z) is reduced to a MINIMUM value.
With minimum Z, current is MAXIMUM for a given voltage.
Maximum current causes maximum voltage drops across the individual reactances.
All of the above follow in sequence from the fact that X
L
= XC at the resonant frequency.