1-9
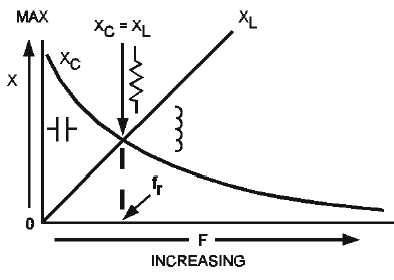
Figure 1-5.—Relationship between XL and XC as frequency increases.
First, note that fr, (the resonant frequency) is that frequency (or point) where the two curves cross. At
this point, and ONLY this point, XL equals XC. Therefore, the frequency indicated by fr is the one and
only frequency of resonance. Note the resistance symbol which indicates that at resonance all reactance is
cancelled and the circuit impedance is effectively purely resistive. Remember, a.c. circuits that are
resistive have no phase shift between voltage and current. Therefore, at resonance, phase shift is
cancelled. The phase angle is effectively zero.
Second, look at the area of the curves to the left of fr. This area shows the relative reactances of the
circuit at frequencies BELOW resonance. To these LOWER frequencies, XC will always be greater than
XL. There will always be some capacitive reactance left in the circuit after all inductive reactance has
been cancelled. Because the impedance has a reactive component, there will be a phase shift. We can also
state that below fr the circuit will appear capacitive.
Lastly, look at the area of the curves to the right of f. This area shows the relative reactances of the
circuit at frequencies ABOVE resonance. To these HIGHER frequencies, XL will always be greater than
XC. There will always be some inductive reactance left in the circuit after all capacitive reactance has
been cancelled. The inductor symbol shows that to these higher frequencies, the circuit will always appear
to have some inductance. Because of this, there will be a phase shift.
RESONANT CIRCUITS
Resonant circuits may be designed as series resonant or parallel resonant. Each has the ability to
discriminate between its resonant frequency and all other frequencies. How this is accomplished by both
series- and parallel-LC circuits is the subject of the next section.
NOTE: Practical circuits are often more complex and difficult to understand than simplified
versions. Simplified versions contain all of the basic features of a practical circuit, but leave out the
nonessential features. For this reason, we will first look at the IDEAL SERIES-RESONANT CIRCUIT—
a circuit that really doesn't exist except for our purposes here.