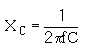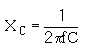1-5
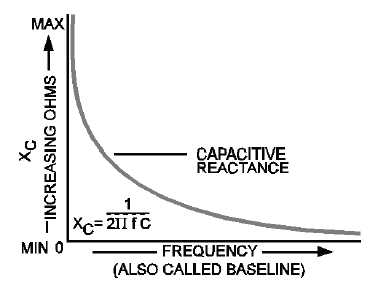
Figure 1-3.—Effect of frequency on capacitive reactance.
Effect of Frequency on Resistance
In the expression for inductive reactance, XL = 2
p
fL, and in the expression for capacitive reactance,
both contain "f" (frequency). Any change of frequency changes the reactance of the circuit components as
already explained. So far, nothing has been said about the effect of frequency on resistance. In an Ohm's
law relationship, such as R = E/I no "f" is involved. Thus, for all practical purposes, a change of
frequency does not affect the resistance of the circuit. If a 60-hertz a.c. voltage causes 20 milliamperes of
current in a resistive circuit, then the same voltage at 2000 hertz, for example, would still cause 20
milliamperes to flow.
NOTE: Remember that the total opposition to a.c. is called impedance (Z). Impedance is the
combination of inductive reactance (XL), capacitive reactance (XC), and resistance (R). When dealing
with a.c. circuits, the impedance is the factor with which you will ultimately be concerned. But, as you
have just been shown, the resistance (R) is not affected by frequency. Therefore, the remainder of the
discussion of a.c. circuits will only be concerned with the reactance of inductors and capacitors and will
ignore resistance.
A.c. Circuits Containing Both Inductive and Capacitive Reactances
A.c. circuits that contain both an inductor and a capacitor have interesting characteristics because of
the opposing effects of L and C. X
L
and XC may be treated as reactors which are 180 degrees out of
phase. As shown in figure 1-2, the vector for XL should be plotted above the baseline; vector for XC,
figure 1-3, should be plotted below the baseline. In a series circuit, the effective reactance, or what is
termed the RESULTANT REACTANCE, is the difference between the individual reactances. As an
equation, the resultant reactance is: