4-43
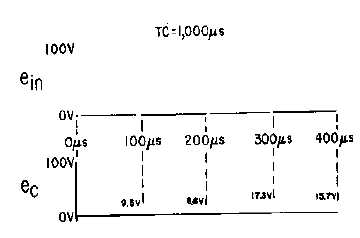
Figure 4-38.—Square wave applied to a long time-constant integrator.
At the first instant of time, 100 volts is applied to the long time-constant circuit. The value of charge
on the capacitor at the end of the first 100 microseconds of the input signal can be found by using the
Universal Time Constant Chart (figure 4-34). Assume that a line is projected up from the point on the
base line corresponding to 0.1TC. The line will intersect the curve at a point that is the percentage of
voltage across the capacitor at the end of the first 100 microseconds. Since the applied voltage is 100
volts, the charge on the capacitor at the end of the first 100 microseconds will be approximately 9.5 volts.
At the end of the first 100 microseconds, the input signal will fall suddenly to 0 and the capacitor will
begin to discharge. It will be able to discharge for 100 microseconds. Therefore, the capacitor will
discharge 9.5 percent of its accumulated 9.5 volts (.095
9.5 = 0.90 volt). The discharge of the 0.90 volt
will result in a remaining charge on the capacitor of 8.6 volts. At the end of 200 microseconds, the input
signal will again suddenly rise to a value of 100 volts. The capacitor will be able to charge to 9.5 percent
of the difference (100
-
8.6 = 91.4 volts). This may also be figured as a value of 8.7 volts plus the initial
8.6 volts. This results in a total charge on the capacitor (at the end of the first 300 microseconds) of 8.7 +
8.6 = 17.3 volts.
Notice that the capacitor voltage at the end of the first 300 microseconds is greater than the capacitor
voltage at the end of the first 100 microseconds. The voltage at the end of the first 100 microseconds is
9.5 volts; the capacitor voltage at the end of the first 300 microseconds is 17.3 volts, an increase of 7.8
volts.
The capacitor charges and discharges in this step-by-step manner until, finally, the capacitor charges
and discharges above and below a 50-volt level. The 50-volt level is controlled by the maximum
amplitude of the square-wave input pulse, the average value of which is 50 volts.
Q21. What is the numerical difference (in terms of the time constant) between a long and a short time-
constant circuit?
Q22. What would happen to the integrator output if the capacitor were made extremely large (all other
factors remaining the same)?
DIFFERENTIATORS
DIFFERENTIATION is the direct opposite of integration. In the RC integrator, the output is taken
from the capacitor. In the differentiator, the output is taken across the resistor. Likewise, this means that
when the RL circuit is used as a differentiator, the differentiated output is taken across the inductor.