4-45
end of the fourth time constant, 2 volts. At the end of the fifth time constant, the voltage across the
resistor will be very close to 0 volts. Since the time constant is equal to 10 microseconds, it will take a
total of 50 microseconds to completely charge the capacitor and stop current flow in the circuit.
As shown in figure 4-40 the slope of the charge curve will be very sharp. The voltage across the
resistor will remain at 0 volts until the end of 100 microseconds. At that time, the applied voltage
suddenly drops to 0, and the capacitor will now discharge through the resistor. At this time, the discharge
current will be maximum causing a large discharge voltage to develop across the resistor. This is shown
as the negative spike in figure 4-40. Since the current flow from the capacitor, which now acts like a
source, is decreasing exponentially, the voltage across the resistor will also decrease. The resistor voltage
will decrease exponentially to 0 volts in 5 time constants. All of this discharge action will take a total of
50 microseconds. The discharge curve is also shown in figure 4-40. At the end of 200 microseconds, the
action begins again. The output waveform taken across the resistor in this short time-constant circuit is an
example of differentiation. With the square wave applied, positive and negative spikes are produced in the
output. These spikes approximate the rate of change of the input square wave.
Medium Time-Constant Differentiator
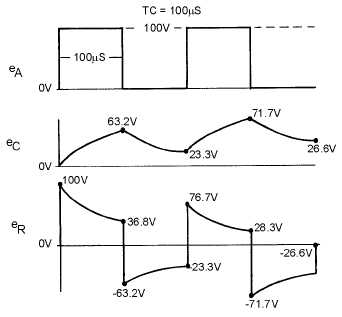
The output across the resistor in an RC circuit of a medium time constant is shown in figure 4-41.
The value of the variable resistor has been increased to a value of 10,000 ohms. This means that the time
constant of the circuit is equal to the duration of the input pulse or 100 microseconds. For clarity, the
voltage waveforms developed across both the resistor and the capacitor are shown. As before, the sum of
the voltages across the resistor and capacitor must be equal to the applied voltage of 100 volts.
Figure 4-41.—Voltage outputs in a medium time-constant differentiator.
At the first instant of time, a pulse of 100 volts in amplitude with a duration of 100 microseconds is
applied. Since the capacitor cannot respond quickly to the change in voltage, all of the applied voltage is
felt across the resistor. Figure 4-41 shows the voltage across the resistor (eR) to be 100 volts and the
voltage across the capacitor (eC) to be 0 volts. As time progresses, the capacitor charges. As the capacitor
voltage increases, the resistor voltage decreases. Since the time that the capacitor is permitted to charge is
100 microseconds (equal to 1TC in this circuit), the capacitor will charge to 63.2 percent of the applied