4-46
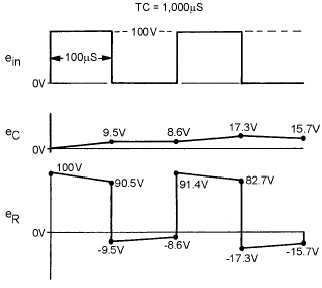
voltage at the end of 1TC, or 63.2 volts. Because Kirchhoff's law must be followed at all times, the
voltage across the resistor must be equal to the difference between the applied voltage and the charge on
the capacitor (100
-
63.2 volts), or 36.8 volts.
At the end of the first 100 microseconds, the input voltage suddenly drops to 0 volts. The charge on
the capacitor (
-
63.2 volts) becomes the source and the entire voltage is developed across the resistor for
the first instant.
The capacitor discharges during the next 100 microseconds. The voltage across the resistor decreases
at the same rate as the capacitor voltage and total voltage is maintained at 0. This exponential decrease in
resistor voltage is shown during the second 100 microseconds in figure 4-41. The capacitor will discharge
63.2 percent of its charge to a value of 23.3 volts at the end of the second 100 microseconds. The resistor
voltage will rise in the positive direction to a value of
-
23.3 volts to maintain the total voltage at 0 volts.
At the end of 200 microseconds, the input voltage again rises suddenly to 100 volts. Since the
capacitor cannot respond to the 100-volt increase instantaneously, the 100-volt change takes place across
the resistor. The voltage across the resistor suddenly rises from
-
23.3 volts to +76.7 volts. The capacitor
will now begin to charge for 100 microseconds. The voltage will decrease across the resistor. This charge
and discharge action will continue for many cycles. Finally, the voltage across the capacitor will rise and
fall by equal amounts both above and below about a 50-volt level. The resistor voltage will also rise and
fall by equal amounts to about a 0-volt level.
Long Time-Constant Differentiator
If the time constant for the circuit in figure 4-39 is increased to make it a long time-constant circuit,
the differentiator output will appear more like the input. The time constant for the circuit can be changed
by either increasing the value of capacitance or resistance. In this circuit, the time constant will be
increased by increasing the value of resistance from 10,000 ohms to 100,000 ohms. Increasing the value
of resistance will result in a time constant of 1,000 microseconds. The time constant is 10 times the
duration of the input pulse. The output of this long time-constant circuit is shown in figure 4-42.
Figure 4-42.—Voltage outputs in a long time-constant differentiator.