4-36
Figure 4-28.—Square wave applied to a resistive circuit.
Figure 4-29.—Square wave applied to an RC circuit.
RC INTEGRATORS
The RC INTEGRATOR is used as a waveshaping network in communications, radar, and
computers. The harmonic content of the square wave is made up of odd multiples of the fundamental
frequency. Therefore SIGNIFICANT HARMONICS (those that have an effect on the circuit) as high as
50 or 60 times the fundamental frequency will be present in the wave. The capacitor will offer a reactance
(XC) of a different magnitude to each of the harmonics
This means that the voltage drop across the capacitor for each harmonic frequency present will not
be the same. To low frequencies, the capacitor will offer a large opposition, providing a large voltage
drop across the capacitor. To high frequencies, the reactance of the capacitor will be extremely small,
causing a small voltage drop across the capacitor. This is no different than was the case for low- and high-
pass filters (discriminators) presented in chapter 1. If the voltage component of the harmonic is not
developed across the reactance of the capacitor, it will be developed across the resistor, if we observe
Kirchhoff's voltage law. The harmonic amplitude and phase relationship across the capacitor is not the
same as that of the original frequency input; therefore, a perfect square wave will not be produced across
the capacitor. You should remember that the reactance offered to each harmonic frequency will cause a
change in both the amplitude and phase of each of the individual harmonic frequencies with respect to the
current reference. The amount of phase and amplitude change taking place across the capacitor depends
on the XC of the capacitor. The value of the resistance offered by the resistor must also be considered
here; it is part of the ratio of the voltage development across the network.
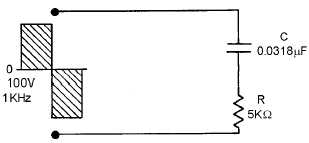
The circuit in figure 4-30 will help show the relationships of R and XC more clearly. The square
wave applied to the circuit is 100 volts peak at a frequency of 1 kilohertz. The odd harmonics will be 3
kilohertz, 5 kilohertz, 7 kilohertz, etc. Table 4-1 shows the values of XC and R offered to several