2-52
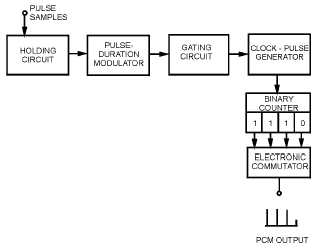
Figure 2-52.—Block diagram of quantizer and pcm coder.
The pcm demodulator will reproduce the correct standard amplitude represented by the pulse-code
group. However, it will reproduce the correct standard only if it is able to recognize correctly the presence
or absence of pulses in each position. For this reason, noise introduces no error at all if the signal-to-noise
ration is such that the largest peaks of noise are not mistaken for pulses. When the noise is random (circuit
and tube noise), the probability of the appearance of a noise peak comparable in amplitude to the pulses
can be determined. This probability can be determined mathematically for any ration of signal-to-average-
noise power. When this is done for 10
5
pulses per second, the approximate error rate for three values of
signal power to average noise power is:
17 dB — 10 errors per second
20 dB — 1 error every 20 minutes
22 dB — 1 error every 2,000 hours
Above a threshold of signal-to-noise ration of approximately 20 dB, virtually no errors occur. In all
other systems of modulation, even with signal-to-noise ratios as high as 60 dB, the noise will have some
effect. Moreover, the pcm signal can be retransmitted, as in a multiple relay link system, as many times as
desired, without the introduction of additional noise effects; that is, noise is not cumulative at relay
stations as it is with other modulation systems.
The system does, of course, have some distortion introduced by quantizing the signal. Both the
standard values selected and the sampling interval tend to make the reconstructed wave depart from the
original. This distortion, called QUANTIZING NOISE, is initially introduced at the quantizing and
coding modulator and remains fixed throughout the transmission and retransmission processes. Its
magnitude can be reduced by making the standard quantizing levels closer together. The relationship of
the quantizing noise to the number of digits in the binary code is given by the following standard
relationship:
Where:
n is the number of digits in the binary code