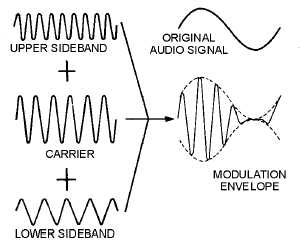
1-44
voltage. The audio intelligence is actually contained in the spacing or difference between the carrier and
sideband frequencies.
Figure 1-39.—Formation of the modulation envelope.
BANDWIDTH OF AN AM WAVE.—An ideal carrier wave contains a single frequency and
occupies very little of the frequency spectrum. When the carrier is amplitude modulated, sideband
frequencies are created both above and below the carrier frequency. This causes the signal to use up a
greater portion of the frequency spectrum. The amount of space in the frequency spectrum required by the
signal is called the BANDWIDTH of the signal.
The bandwidth of a modulated wave is a function of the frequencies contained in the modulating
signal. For example, when a 100-kilohertz carrier is modulated by a 5-kilohertz audio tone, sideband
frequencies are created at 95 and 105 kilohertz. This signal requires 10 kilohertz of space in the spectrum.
If the same 100-kilohertz carrier is modulated by a 10-kilohertz audio tone, sideband frequencies will
appear at 90 and 110 kilohertz and the signal will have a bandwidth of 20 kilohertz. Notice that as the
modulating signal becomes higher in frequency, the bandwidth required also becomes greater. As
illustrated by the above examples, the bandwidth of an amplitude-modulated wave at any instant is two
times the highest modulating frequency applied at that time. Thus, if a 400-kilohertz carrier is modulated
with 3, 5, and 8 kilohertz simultaneously, sideband frequencies will appear at 392, 395, 397, 403, 405,
and 408 kilohertz. This signal extends from 392 to 408 kilohertz and has a bandwidth of 16 kilohertz,
twice the highest modulating frequency of 8 kilohertz.
Musical instruments produce complex sound waves containing a great number of frequencies. The
frequencies produced by a piano, for example, range from approximately 27 to 4,200 hertz with harmonic
frequencies extending beyond 10 kilohertz. Modulating frequencies of up to 15 kilohertz must be
included in the signal to transmit a musical passage with a high degree of fidelity. This requires a
bandwidth of at least 30 kilohertz to prevent attenuation of higher-order harmonic frequencies.
If the signal to be transmitted contains voice frequencies only, and fidelity is of minor importance,
the bandwidth requirement is much smaller. A baritone voice includes frequencies of approximately 100
to 350 hertz, or 250 hertz. Intelligible voice communications can be carried out as long as the
communications system retains audio frequencies up to several thousand hertz. Comparing the conditions