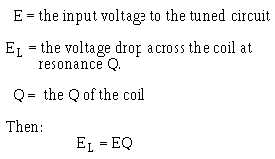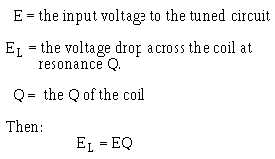1-25
The Q of a Coil
Q is a feature that is designed into a coil. When the coil is used within the frequency range for which
it is designed, Q is relatively constant. In this sense, it is a physical characteristic.
Inductance is a result of the physical makeup of a coil - number of turns, core, type of winding, etc.
Inductance governs reactance at a given frequency. Resistance is inherent in the length, size, and material
of the wire. Therefore, the Q of a coil is mostly dependent on physical characteristics.
Values of Q that are in the hundreds are very practical and often found in typical equipment.
Application of Q
For the most part, Q is the concern of designers, not technicians. Therefore, the chances of you
having to figure the Q of a coil are remote. However, it is important for you to know some circuit
relationships that are affected by Q.
Q Relationships in Series Circuits
Q can be used to determine the "gain" of series-resonant circuits. Gain refers to the fact that at
resonance, the voltage drop across the reactances are greater than the applied voltage. Remember, when
we applied Ohm's law in a series-resonant circuit, it gave us the following characteristics:
Low impedance, high current.
High current; high voltage across the comparatively high reactances.
This high voltage is usable where little power is required, such as in driving the grid of a vacuum
tube or the gate of a field effect transistor (F.E.T.). The gain of a properly designed series-resonant circuit
may be as great or greater than the amplification within the amplifier itself. The gain is a function of Q, as
shown in the following example:
If the Q of the coil were 100, then the gain would be 100; that is, the voltage of the coil would be 100
times that of the input voltage to the series circuit.
Resistance affects the resonance curve of a series circuit in two ways — the lower the resistance, the
higher the current; also, the lower the resistance, the sharper the curve. Because low resistance causes
high Q, these two facts are usually expressed as functions of Q. That is, the higher the Q, the higher and
sharper the curve and the more selective the circuit.
The lower the Q (because of higher resistance), the lower the current curve; therefore, the broader
the curve, the less selective the circuit. A summary of the major characteristics of series RLC-circuits at
resonance is given in table 1-1.