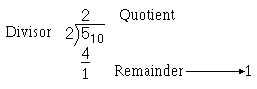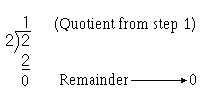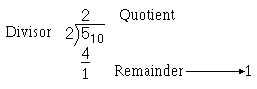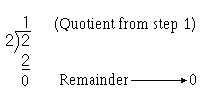1-39
The sections of this chapter that discussed octal and hex numbers both mentioned that their number
systems were beneficial to programmers. You will see later in this section that octal and hex numbers are
easily converted to binary numbers and vice versa..
If you are going to work with computers, there will be many times when it will be necessary to
convert decimal numbers to binary, octal, and hex numbers. You will also have to be able to convert
binary, octal, and hex numbers to decimal numbers. Converting each number system to each of the others
will be explained. This will prepare you for converting from any base to any other base when needed.
DECIMAL CONVERSION
Some computer systems have the capability to convert decimal numbers to binary numbers. They do
this by using additional circuitry. Many of these systems require that the decimal numbers be converted to
another form before entry.
Decimal to Binary
Conversion of a decimal number to any other base is accomplished by dividing the decimal number
by the radix of the system you are converting to. The following definitions identify the basic terms used
in division:
DIVIDENDThe number to be divided
DIVISORThe number by which a dividend is divided
QUOTIENTThe number resulting from the division of one number by another
REMAINDERThe final undivided part after division that is less or of a lower degree than the
divisor
To convert a base 10 whole number to its binary equivalent, first set up the problem for division:
Step 1—Divide the base 10 number by the radix (2) of the binary system and extract the remainder
(this becomes the binary number's LSD).
Step 2—Continue the division by dividing the quotient of step 1 by the radix (2