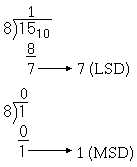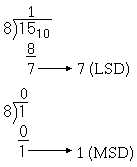1-43
Although the multiplication was carried out for seven places, you would only use what is required.
Write out the solution as shown:
.011012
To convert a mixed number such as 37.62510 to binary, split the number into its whole and fractional
components and solve each one separately. In this problem carry the fractional part to four places. When
the conversion of each is completed, recombine it with the radix point as shown below:
3710 = 1001012
.62510 = .10102
37.62510 = 100101.10102
Convert the following decimal numbers to binary:
Q48.
7210.
Q49.
9710.
Q50.
24310.
Q51.
0.87510 (four places).
Q52.
0.3310 (four places).
Q53.
17.4210 (five places)
Decimal to Octal
The conversion of a decimal number to its base 8 equivalent is done by the repeated division method.
You simply divide the base 10 number by 8 and extract the remainders. The first remainder will be the
LSD, and the last remainder will be the MSD.
Look at the following example. To convert 1510 to octal, set up the problem for division:
Since 8 goes into 15 one time with a 7 remainder, 7 then is the LSD. Next divide 8 into the quotient
(1). The result is a 0 quotient with a 1 remainder. The 1 is the MSD: