3-10
Q12. What is the output of C1?
SUBTRACTION
Subtraction is accomplished in computers by the R’s complement and add method. This is the same
method you used in chapter 1 to subtract binary numbers.
R’s complement subtraction allows us to use fewer circuits than would be required for separate add
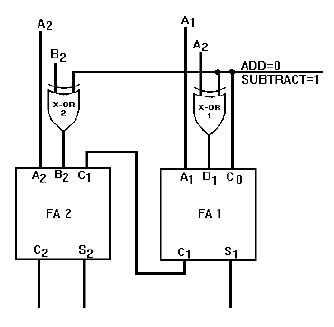
and subtract functions. Adding X-OR gates to full adders, as shown in figure 3-11, enables the circuit to
perform R’s complement subtraction as well as addition.
Figure 3-11. —R's complement adder/subtracter.
To add two numbers using this circuit, the addend and augend are applied to the A and B inputs. The
B inputs are applied to one input of the X-OR gates. A control signal is applied to the other input of the
X-OR gates. When the control signal is LOW, the circuit will add; and when it is HIGH, the circuit will
subtract.
In the add mode, the outputs of the X-OR gates will be the same as the B inputs. Addition takes
place in the same manner as described in parallel addition.
Before we attempt to show subtraction, let’s review R’s complement subtraction. To subtract 102
from 112, write down the minuend (112). Perform the R’s complement on the subtrahend. Now add the
minuend and the complemented subtrahend.
112 minuend
+ 102 R’s complement
101 Difference
Disregard the most significant 1, and the difference between 112 and 102 is 012. The most significant
1 will not be used in the example shown in the following paragraph.