3-8
When A, B, and the carry-in are all HIGH, a sum of 1 and a carry-out are produced. First, consider A
and B. When both are HIGH, the output of gate 1 is LOW, and the output of gate 2 is HIGH, giving us a
carry-out at gate 5. The carry-in produces a 1 output at gate 3, giving us a sum of 1. The output of the full
adder is 112. The sum of 12 plus 12 plus 12 is 112.
PARALLEL ADDERS
The adders discussed in the previous section have been limited to adding single-digit binary numbers
and carries. The largest sum that can be obtained using a full adder is 112.
Parallel adders let us add multiple-digit numbers. If we place full adders in parallel, we can add two-
or four-digit numbers or any other size desired.
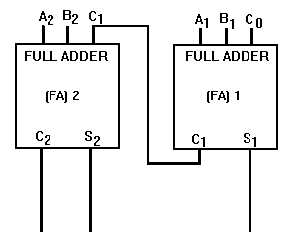
Figure 3-9 uses STANDARD SYMBOLS to show a parallel adder capable of adding two, two-digit
binary numbers. In previous discussions we have depicted circuits with individual logic gates shown.
Standard symbols (blocks) allow us to analyze circuits with inputs and outputs only. One standard symbol
may actually contain many and various types of gates and circuits. The addend would be input on the A
inputs (A2 = MSD, A1 = LSD), and the augend input on the B inputs (B2 = MSD, B1 = LSD). For this
explanation we will assume there is no input to C0 (carry from a previous circuit).
Figure 3-9. —Parallel binary adder.
Now let’s add some two-digit numbers. To add 102 (addend) and 012 (augend), assume there are
numbers at the appropriate inputs. The addend inputs will be 1 on A2 and 0 on A1. The augend inputs will
be 0 on B2 and 1 on B1. Working from right to left, as we do in normal addition, let’s calculate the outputs
of each full adder.
With A1 at 0 and B1 at 1, the output of adder 1 will be a sum (S1) of 1 with no carry (C1). Since A2 is
1 and B2 is 0, we have a sum (S2) of 1 with no carry (C2) from adder 1. To determine the sum, read the
outputs (C2, S
2, and S1) from left to right. In this case, C2 = 0, S2 = 1, and S1 = 1. The sum, then, of 102
and 012 is 0112 or 112.
To add 112 and 012, assume one number is applied to A1 and A2, and the other to B1 and B2, as
shown in figure 3-10. Adder 1 produces a sum (S1) of 0 and a carry (C1) of 1. Adder 2 gives us a sum (S2)