3-7
We have seen that the output of the quarter adder is HIGH when either input, but not both, is HIGH.
It is only when both inputs are HIGH that the AND gate is activated and a carry is produced. The largest
sum that can be obtained from a half adder is 102 (12 plus 12).
FULL ADDER
The full adder becomes necessary when a carry input must be added to the two binary digits to
obtain the correct sum. A half adder has no input for carries from previous circuits.
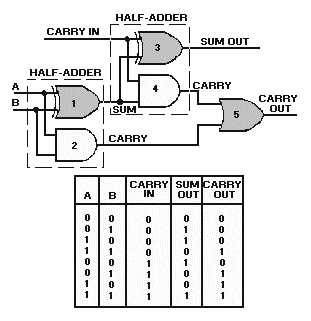
One method of constructing a full adder is to use two half adders and an OR gate as shown in figure
3-8. The inputs A and B are applied to gates 1 and 2. These make up one half adder. The sum output of
this half adder and the carry-from a previous circuit become the inputs to the second half adder. The carry
from each half adder is applied to gate 5 to produce the carry-out for the circuit.
Figure 3-8. —Full adder and Truth Table.
Now let’s add a series of numbers and see how the circuit operates.
First, let’s add 1 and 0. When either A or B is HIGH, gate 1 has an output. This output is applied to
gates 3 and 4. Since the carry-in is 0, only gate 3 will produce an output. The sum of 12 and 0 is 12.
Now let’s add 12 and 12. If A and B are both HIGH, the output of gate 1 is LOW. When the carry-in
is 0 (LOW), the output of gate 3 is LOW. Gate 2 produces an output that is applied to gate 5, which
produces the carry-out. The sum of 12 and 12 is 102, just as it was for the half adder.
When A and B are both LOW and the carry-in is 1, only gate 3 has an output and produces a sum of
12 with no carry-out.
Now, let’s add A or B and a carry-in. For example, let’s assume that A is HIGH and B is LOW. With
these conditions, gate 1 will have an output. This output and the carry-in applied to gates 3 and 4 will
produce a sum out of 0 and a carry of 1. This carry from gate 4 will cause gate 5 to produce a carry-out.
The sum of A and a carry (12 plus 12) is 102.