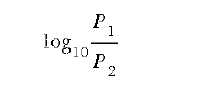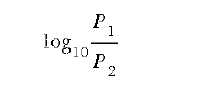2-2
Power measurements for af circuits are usually indicated in terms of decibels (dB) or decibels
referenced to 1 milliwatt (dBm). Because the actual calculation of decibel measurements is seldom
required, the following explanation is somewhat simplified. Most test equipment is designed to measure
and indicate decibels directly. This eliminates the need for you to perform complicated calculations.
Nevertheless, a basic explanation of the decibel measurement system is necessary for you to understand
the significance of dB readings and amplifier-gain ratings that are expressed in decibels.
THE DECIBEL SYSTEM
The basic unit of measurement in the system is not the decibel; it is the bel. The bel is a unit that
expresses the logarithmic ratio between the input and the output of any given component, circuit, or
system. It may be expressed in terms of voltage, current, or power. Most often, it is used to show the ratio
between input and output power to figure gain. You can express the power gain of the amplifier (N) in
bels by dividing the output (P1) by the input (P2) and taking the base 10 logarithm of the resulting
quotient. The formula for determining this gain is:
If an amplifier doubles the input power, the quotient of P1 to P2 will be 2. If you consult a logarithm
table, you will find that the base 10 logarithm of 2 is 0.3, making the power gain of the amplifier 0.3 bel.
Q-1. What is the logarithmic ratio between the input and output of a given circuit called?
Experience has shown that because the bel is a rather large unit, it is difficult to apply. A more
practical unit, and one that can be used more easily, is the decibel (1/10 bel). You can convert any figure
expressed in bels to decibels by multiplying that figure by 10 or simply by moving the decimal point one
place to the right. Applying this rule, we find that the above ratio of 0.3 bel is equal to 3 decibels.
The decibel (dB) cannot be used to represent actual power; only the ratio of one power compared to
another. To say that an amplifier has a 3 dB gain means that the output power is twice the input power.
This gives no indication of the actual power represented. You must be able to state the input power for it
to be meaningful. In many applications, a mathematical expression represents the actual power, not a
power ratio. One standard reference is the dBm.
The dBm is an abbreviation used to represent power levels above or below 1 milliwatt. Negative
dBm (-dBm) represents power levels below 1 milliwatt, and positive dBm (+dBm) represents power
levels above 1 milliwatt. In other words, a dBm value is a specific amount of power; 0 dBm is equal to 1
milliwatt. Briefly stated, the amount of power in a given value of dBm is the power which results if 1
milliwatt is amplified or attenuated by that dB value. For example, 40 dBm represents an actual power
level (watts or milliwatts) that is 40 dB above 1 milliwatt, whereas -10 dBm represents a power level that
is 10 dB below 1 milliwatt. The formula for finding dBm is a variation of the dB power formula:
Q-2. What term is used to represent power levels above or below a 1-milliwatt reference?