3-8
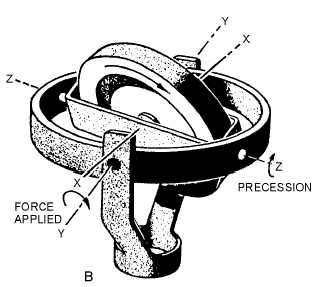
Figure 3-7B.—Gyro action.
Regardless of how the fork is placed, the spinning gyro wheel is free to lie in any given plane. That's
why it is called a free gyroscope in this type of mounting.
To show the effect of precession, we can push down on the gimbal ring at point A at the nearer end
of the Z-Z axis. (See view A of figure 3-7.) You might expect the ring to tilt around the Y-Y axis. Instead,
the gyro case will tilt about the Z-Z axis. You can see the effect of this precession in view B.
Here's a rule that applies to all spinning gyros: THE GYRO WILL ALWAYS PRECESS AT RIGHT
ANGLES TO THE DIRECTION OF THE APPLIED FORCE. Look at view A again. If we keep pushing
down on the gimbal ring at point (A), the gyro case will keep turning until the spin axis of the gyro wheel
is horizontal. Then there will be no further precession. At this point the gyro wheel will be spinning in the
same direction in which the applied force is pushing.
Here's another rule: A GYRO ALWAYS PRECESSES IN A DIRECTION TENDING TO LINE
ITSELF UP SO THAT ITS ROTOR SPINS IN THE SAME DIRECTION THAT THE APPLIED
FORCE IS TRYING TO TURN IT. In other words, the direction of spin chases the applied force. When
the direction of spin and the applied force are in the same direction, precession stops.
Now, compare the spin (X) axis in the two parts of figure 3-7. In view A, the spin axis is vertical. In
view B, the spin axis has moved from the vertical until it is much closer to being horizontal. By applying
the right amount of force in the right place, we have a method of "aiming" the spin axis so that it points to
the specific fixed direction in space where we want it. The property of PRECESSION makes the property
of RIGIDITY useable.
You should understand that most forces, when applied to the gyro mounting, do not cause
precession. For instance, you can swing the fork around in any direction, and the motion will merely be
taken up in the Y-Y and Z-Z axes. Similarly, a force applied lengthwise along one of the axes will have
no effect.
Any force acting through the center of gravity of the gyroscope does not change the angle of the
plane of rotation but moves the gyroscope as a unit. The position of its spin axis in space is not changed.
Such forces as those stated above, operating through the center of gravity, are forces of TRANSLATION.
In other words, the spinning gyroscope may be moved freely in space by means of its supporting frame,