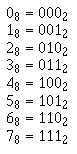1-48
BINARY CONVERSION
Earlier in this chapter, we mentioned that the octal and hex number systems are useful to computer
programmers. It is much easier to provide data to a computer in one or the other of these systems.
Likewise, it is important to be able to convert data from the computer into one or the other number
systems for ease of understanding the data.
Binary to Octal
Look at the following numbers:
101110010011012
271158
You can easily see that the octal number is much easier to say. Although the two numbers look
completely different, they are equal.
Since 8 is equal to 23, then one octal digit can represent three binary digits, as shown below:
With the use of this principle, the conversion of a binary number is quite simple. As an example,
follow the conversion of the binary number at the beginning of this section.
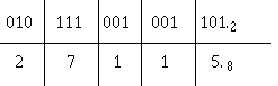
Write out the binary number to be converted. Starting at the radix point and moving left, break the
binary number into groups of three as shown. This grouping of binary numbers into groups of three is
called binary-coded octal (BCO). Add 0s to the left of any MSD that will fill a group of three:
Next, write down the octal equivalent of each group: