1-51
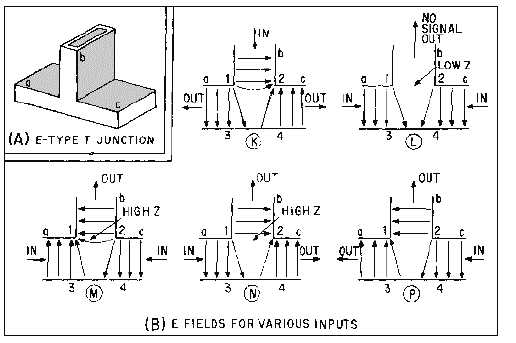
Figure 1-64, view (B), illustrates cross-sectional views of the E-type T junction with inputs fed into
the various arms. For simplicity, the magnetic lines that are always present with an electric field have
been omitted. In view (K), the input is fed into arm b and the outputs are taken from the a and c arms.
When the E field arrives between points 1 and 2, point 1 becomes positive and point 2 becomes negative.
The positive charge at point 1 then induces a negative charge on the wall at point 3. The negative charge
at point 2 induces a positive charge at point 4. These charges cause the fields to form 180 degrees out of
phase in the main waveguide; therefore, the outputs will be 180 degrees out of phase with each other. In
view (L), two in-phase inputs of equal amplitude are fed into the a and c arms. The signals at points 1 and
2 have the same phase and amplitude. No difference of potential exists across the entrance to the b arm,
and no energy will be coupled out. However, when the two signals fed into the a and c arms are 180
degrees out of phase, as shown in view (M), points 1 and 2 have a difference of potential. This difference
of potential induces an E field from point 1 to point 2 in the b arm, and energy is coupled out of this arm.
Views (N) and (P) illustrate two methods of obtaining two outputs with only one input.
Figure 1-64.—E fields in an E-type T junction.
H-TYPE T JUNCTION.—An H-type T junction is illustrated in figure 1-65A. It is called an H-type
T junction because the long axis of the "b" arm is parallel to the plane of the magnetic lines of force in the
waveguide. Again, for simplicity, only the E lines are shown in this figure. Each X indicates an E line
moving away from the observer. Each dot indicates an E line is moving toward the observer.
In view (1) of figure 1-65B, the signal is fed into arm b and in-phase outputs are obtained from the a
and c arms. In view (2), in-phase signals are fed into arms a and c and the output signal is obtained from
the b arm because the fields add at the junction and induce E lines into the b arm. If 180-degree-out-of-
phase signals are fed into arms a and c, as shown in view (3), no output is obtained from the b arm
because the opposing fields cancel at the junction. If a signal is fed into the a arm, as shown in view (4),
outputs will be obtained from the b and c arms. The reverse is also true. If a signal is fed into the c arm,
outputs will be obtained from the a and b arms.