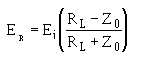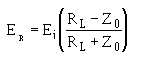3-45
TERMINATION IN A SHORT CIRCUIT
On the line terminated in a short circuit, shown in figure 3-34, view D, the voltage is zero at the end
DQG PD[LPXP DW IURP WKH HQG 7KH FXUUHQW LV PD[LPXP DW WKH HQG ]HUR DW IURP WKH HQG DQG
DOWHUQDWHO\ PD[LPXP DQG ]HUR HYHU\ WKHUHDIWHU
TERMINATION IN CAPACITANCE
When a line is terminated in capacitance, the capacitor does not absorb energy, but returns all of the
energy to the circuit. This means there is 100 percent reflection. The current and voltage relationships are
somewhat more involved than in previous types of termination. For this explanation, assume that the
capacitive reactance is equal to the Z0 of the line. Current and voltage are in phase when they arrive at the
end of the line, but in flowing through the capacitor and the characteristic impedance (Z0) connected in
series, they shift in phase relationship. Current and voltage arrive in phase and leave out of phase. This
results in the standing-wave configuration shown in figure 3-34, view E. The standing wave of voltage is
PLQLPXP DW D GLVWDQFH RI H[DFWO\ IURP WKH HQG ,I WKH FDSDFLWLYH UHDFWDQFH LV JUHDWHU WKDQ =0 (smaller
capacitance), the termination looks more like an open circuit; the voltage minimum moves away from the
end. If the capacitive reactance is smaller than Z0, the minimum moves toward the end.
TERMINATION IN INDUCTANCE
When the line is terminated in an inductance, both the current and voltage shift in phase as they
arrive at the end of the line. When XL is equal to Z0, the resulting standing waves are as shown in figure
3 YLHZ ) 7KH FXUUHQW PLQLPXP LV ORFDWHG IURP WKH HQG RI WKH OLQH :KHQ WKH LQGXFWLYH UHDFWDQFH
is increased, the standing waves appear closer to the end. When the inductive reactance is decreased, the
standing waves move away from the end of the line.
TERMINATION IN A RESISTANCE NOT EQUAL TO THE CHARACTERISTIC IMPEDANCE
(Z0)
Whenever the termination is not equal to Z0, reflections occur on the line. For example, if the
terminating element contains resistance, it absorbs some energy, but if the resistive element does not
equal the Z0 of the line, some of the energy is reflected. The amount of voltage reflected may be found by
using the equation:
Where:
ER = the reflected voltage
Ei = the incident voltage
RR = the terminating resistance
Z0= the characteristic impedance of the line
If you try different values of RL in the preceding equation, you will find that the reflected voltage is
equal to the incident voltage only when RL equals 0 or is infinitely large. When RL equals Z0, no reflected
voltage occurs. When RL is greater than Z0, ER is positive, but less than Ei. As RL increases and