1-22
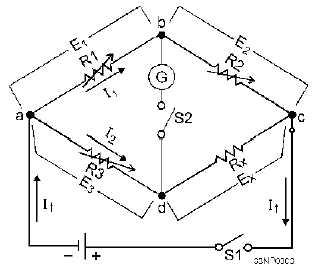
Figure 1-5.—Wheatstone bridge.
The operation of the bridge is explained in a few logical steps. When the battery switch S1 is closed,
electrons flow from the negative terminal of the battery to point a. Here the current divides as it would in
any parallel circuit. Part of it passes through R1 and R2; the remainder passes through R3 and Rx. The
two currents, I1 and I2, unite at point c and return to the positive terminal of the battery. The value of I1
depends on the sum of resistance R1 and R2, and the value of I2 depends on the sum of resistances R3 and
Rx. In each case, according to Ohm’s law, the current is inversely proportional to the resistance.
R1, R2, and R3 are adjusted so that when S1 is closed, no current flows through G. When the
galvanometer shows no deflection, there is no difference of potential between points b and d. All of I
1
follows the a b c path and all I2 follows the a b c path. This means that a voltage drop E1 (across R1
between points a and b) is the same as voltage drop E3 (across R3 between points a and d). Similarly, the
voltage drops across R2 and Rx (E2 and Ex) are also equal. Expressed algebraically,
and
With this information, we can figure the value of the unknown resistor Rx. Divide the voltage drops
across R1 and R3 by their respective voltage drops across R2 and Rx as follows:
We can simplify this equation: