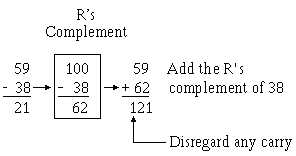
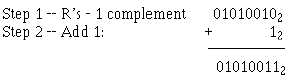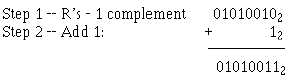1-20
Now let’s look at the number system that most computers use, the binary system. Just as the decimal
system, had the nines (R’s-1) and tens (R’s) complement, the binary system has two types of complement
methods. These two types are the ones (R’s-1) complement and the twos (R’s) complement. The binary
system R’s-1 complement is the difference between the binary number and all 1s. The R’s complement is
the difference between the binary number and the next higher power of 2.
Let’s look at a quick and easy way to form the R’s-1 complement. To do this, change each 1 in the
original number to 0 and each 0 in the original number to 1 as has been done in the example below.
10110112
1001002 R’s-1 complement
There are two methods of achieving the R’s complement. In the first method we perform the R’s-1
complement and then add 1. This is much easier than subtracting the original number from the next higher
power of 2. If you had subtracted, you would have had to borrow.
Saying it another way, to reach the R’s complement of any binary number, change all 1s to 0s and all
0s to 1s, and then add 1.
As an example let’s determine the R’s complement of 101011012:
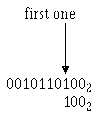
The second method of obtaining the R’s complement will be demonstrated on the binary number
001011011002.
Step 1—Start with the LSD, working to the MSD, writing the digits as they are up to and including
the first one.