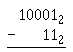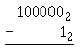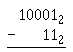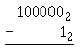1-19
Q18.
Subtract:
Q19.
Subtract:
Q20.
Subtract:
Complementary Subtraction
If you do any work with computers, you will soon find out that most digital systems cannot
subtractthey can only add. You are going to need a method of adding that gives the results of
subtraction. Does that sound confusing? Really, it is quite simple. A COMPLEMENT is used for our
subtractions. A complement is something used to complete something else.
In most number systems you will find two types of complements. The first is the amount necessary
to complete a number up to the highest number in the number system. In the decimal system, this would
be the difference between a given number and all 9s. This is called the nines complement or the radix-1 or
R’s-1 complement. As an example, the nines complement of 254 is 999 minus 254, or 745.
The second type of complement is the difference between a number and the next higher power of the
number base. As an example, the next higher power of 10 above 999 is 1,000. The difference between
1,000 and 254 is 746. This is called the tens complement in the decimal number system. It is also called
the radix or R’s complement. We will use complements to subtract. Let’s look at the magic of this process.
There are three important points we should mention before we start: (1) Never complement the minuend
in a problem, (2) always disregard any carry beyond the number of positions of the largest of the original
numbers, and (3) add the R’s complement of the original subtrahend to the original minuend. This will
have the same effect as subtracting the original number. Let’s look at a base ten example in which we
subtract 38 from 59: