2-49
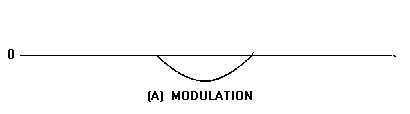
Figure 2-48A.—Quantization levels. MODULATION.
Figure 2-48B.—Quantization levels. TIMING.
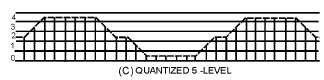
Figure 2-48C.—Quantization levels. QUANTIZED 5-LEVEL.
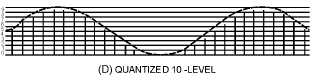
Figure 2-48D.—Quantization levels. QUANTIZED 10-LEVEL.
Although the quantization curves of figure 2-48 are based on 5- and 10-level quantization, in actual
practice the levels are usually established at some exponential value of 2, such as 4(22), 8(2
3), 16(24),
32(25) . . . N(2n). The reason for selecting levels at exponential values of 2 will become evident in the
discussion of pcm. Quantized fm is similar in every way to quantized AM. That is, the range of frequency
deviation is divided into a finite number of standard values of deviation. Each sampling pulse results in a
deviation equal to the standard value nearest the actual deviation at the sampling instant. Similarly, for
phase modulation, quantization establishes a set of standard values. Quantization is used mostly in
amplitude- and frequency-modulated pulse systems.
Figure 2-49 shows the relationship between decimal numbers, binary numbers, and a pulse-code
waveform that represents the numbers. The table is for a 16-level code; that is, 16 standard values of a
quantized wave could be represented by these pulse groups. Only the presence or absence of the pulses
are important. The next step up would be a 32-level code, with each decimal number represented by a
series of five binary digits, rather than the four digits of figure 2-49. Six-digit groups would provide a
64-level code, seven digits a 128-level code, and so forth. Figure 2-50 shows the application of
pulse-coded groups to the standard values of a quantized wave.