1-3
Each of the number systems you will study is built around the following components: the UNIT,
NUMBER, and BASE (RADIX).
Unit and Number
The terms unit and number when used with the decimal system are almost self-explanatory. By
definition the unit is a single object; that is, an apple, a dollar, a day. A number is a symbol representing a
unit or a quantity. The figures 0, 1, 2, and 3 through 9 are the symbols used in the decimal system. These
symbols are called Arabic numerals or figures. Other symbols may be used for different number systems.
For example, the symbols used with the Roman numeral system are letters V is the symbol for 5, X for
10, M for 1,000, and so forth. We will use Arabic numerals and letters in the number system discussions
in this chapter.
Base (Radix)
The base, or radix, of a number system tells you the number of symbols used in that system. The
base of any system is always expressed in decimal numbers. The base, or radix, of the decimal system is
10. This means there are 10 symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 used in the system. A number
system using three symbols 0, 1, and 2 would be base 3; four symbols would be base 4; and so
forth. Remember to count the zero or the symbol used for zero when determining the number of symbols
used in a number system.
The base of a number system is indicated by a subscript (decimal number) following the value of the
number. The following are examples of numerical values in different bases with the subscript to indicate
the base:
759210 2145 1234 6567
You should notice the highest value symbol used in a number system is always one less than the base
of the system. In base 10 the largest value symbol possible is 9; in base 5 it is 4; in base 3 it is 2.
Positional Notation and Zero
You must observe two principles when counting or writing quantities or numerical values. They are
the POSITIONAL NOTATION and the ZERO principles.
Positional notation is a system where the value of a number is defined not only by the symbol but by
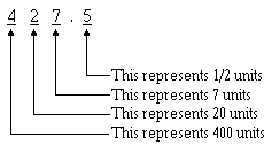
the symbol’s position. Let’s examine the decimal (base 10) value of 427.5. You know from experience that
this value is four hundred twenty-seven and one-half. Now examine the position of each number:
If 427.5 is the quantity you wish to express, then each number must be in the position shown. If you
exchange the positions of the 2 and the 7, then you change the value.