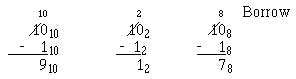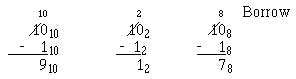1-29
In each example, you cannot subtract 1 from 0 and have a positive difference. You must use a
borrow from the next column of numbers. Let’s examine the above problems and show the borrow as a
decimal quantity for clarity:
When you use the borrow, the column you borrow from is reduced by 1, and the amount of the
borrow is added to the column of the minuend being subtracted. The following examples show this
procedure:
In the octal example 78 cannot be subtracted from 68, so you must borrow from the 4. Reduce the 4
by 1 and add 108 (the borrow) to the 68 in the minuend. By subtracting 78 from 168, you get a difference of
78. Write this number in the difference line and bring down the 3. You may need to refer to table 1-4, the
octal addition table, until you are familiar with octal numbers. To use the table for subtraction, follow
these directions. Locate the subtrahend in column Y. Now find where this line intersects with the minuend
in area Z. The remainder, or difference, will be in row X directly above this point.
Do the following problems to practice your octal subtraction:
Q30.
Subtract:
Q31.
Subtract: