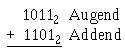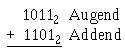1-13
The sum of each of the first three combinations is obvious:
0 + 0 = 02
0 + 1 = 12
1 + 0 = 12
The fourth combination presents a different situation. The sum of 1 and 1 in any other number
system is 2, but the numeral 2 does not exist in the binary system. Therefore, the sum of 12 and 12 is 102
(spoken as one zero base two), which is equal to 210.
Study the following examples using the four combinations mentioned above:
When a carry is produced, it is noted in the column of the next higher value or in the column
immediately to the left of the one that produced the carry.
Example: Add 10112 and 11012.
Solution: Write out the problem as shown:
As we noted previously, the sum of 1 and 1 is 2, which cannot be expressed as a single digit in the
binary system. Therefore, the sum of 1 and 1 produces a carry: