3-14
CHARACTERISTIC IMPEDANCE OF A TRANSMISSION LINE
You learned earlier that the maximum (and most efficient) transfer of electrical energy takes place
when the source impedance is matched to the load impedance. This fact is very important in the study of
transmission lines and antennas. If the characteristic impedance of the transmission line and the load
impedance are equal, energy from the transmitter will travel down the transmission line to the antenna
with no power loss caused by reflection.
Definition and Symbols
Every transmission line possesses a certain CHARACTERISTIC IMPEDANCE, usually designated
as Z0. Z0 is the ratio of E to I at every point along the line. If a load equal to the characteristic impedance
is placed at the output end of any length of line, the same impedance will appear at the input terminals of
the line. The characteristic impedance is the only value of impedance for any given type and size of line
that acts in this way. The characteristic impedance determines the amount of current that can flow when a
given voltage is applied to an infinitely long line. Characteristic impedance is comparable to the
resistance that determines the amount of current that flows in a dc circuit.
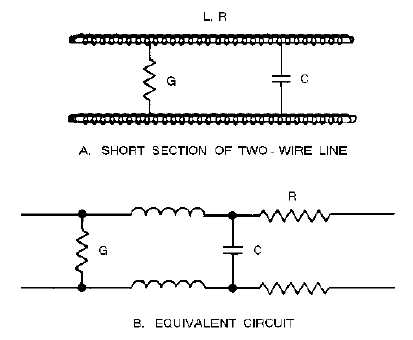
In a previous discussion, lumped and distributed constants were explained. Figure 3-15, view A,
shows the properties of resistance, inductance, capacitance, and conductance combined in a short section
of two-wire transmission line. The illustration shows the evenly distributed capacitance as a single
lumped capacitor and the distributed conductance as a lumped leakage path. Lumped values may be used
for transmission line calculations if the physical length of the line is very short compared to the
wavelength of energy being transmitted. Figure 3-15, view B, shows all four properties lumped together
and represented by their conventional symbols.
Figure 3-15.—Short section of two-wire transmission line and equivalent circuit.
Q19. Describe the leakage current in a transmission line and in what unit it is expressed.