1-2
SQUARE MIL
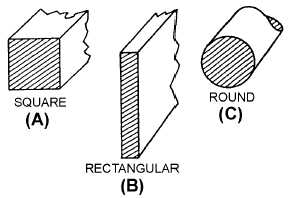
The square mil is a unit of measurement used to determine the cross-sectional area of a square or
rectangular conductor (views A and B of figure 1-1). A square mil is defined as the area of a square, the
sides of which are each 1 mil. To obtain the cross-sectional area of a square conductor, multiply the
dimension of any side of the square by itself. For example, assume that you have a square conductor with
a side dimension of 3 mils. Multiply 3 mils by itself (3 mils 3 mils). This gives you a cross-sectional
area of 9 square mils.
Figure 1-1.—Cross-sectional areas of conductors.
Q1.
State the reason for the establishment of a "unit size" for conductors.
Q2.
Calculate the diameter in MILS of a conductor that has a diameter of 0.375 inch.
Q3.
Define a mil-foot.
To determine the cross-sectional area of a rectangular conductor, multiply the length times the width
of the end face of the conductor (side is expressed in mils). For example, assume that one side of the
rectangular cross-sectional area is 6 mils and the other side is 3 mils. Multiply 6 mils 3 mils, which
equals 18 square mils. Here is another example. Assume that a conductor is 3/8 inch thick and 4 inches
wide. The 3/8 inch can be expressed in decimal form as 0.375 inch. Since 1 mil equals 0.001 inch, the
thickness of the conductor will be 0.001 0.375, or 375 mils. Since the width is 4 inches and there are
1,000 mils per inch, the width will be 4 1,000, or 4,000 mils. To determine the cross-sectional area,
multiply the length by the width; or 375 mils 4,000 mils. The area will be 1,500,000 square mils.
Q4. Define a square mil as it relates to a square conductor.
CIRCULAR MIL
The circular mil is the standard unit of measurement of a round wire cross-sectional area (view C of
figure 1-1). This unit of measurement is found in American and English wire tables. The diameter of a
round conductor (wire) used to conduct electricity may be only a fraction of an inch. Therefore, it is
convenient to express this diameter in mils to avoid using decimals. For example, the diameter of a wire is
expressed as 25 mils instead of 0.025 inch. A circular mil is the area of a circle having a diameter of 1
mil, as shown in view B of figure 1-2. The area in circular mils of a round conductor is obtained by
squaring the diameter, measured in mils. Thus, a wire having a diameter of 25 mils has an area of 252, or
625 circular mils. To determine the number of square mils in the same conductor, apply the conventional
formula for determining the area of a circle (A = pr2). In this formula, A (area) is the unknown and is
equal to the cross-sectional area in square mils, p is the constant 3.14, and r is the radius of the circle, or
half the diameter (D). Through substitution, A = 3.14, and (12.5)
2; therefore, 3.14 156.25 = 490.625